leetcode-每日一题-No.2974. 最小数字游戏

题目

你有一个下标从 0 开始、长度为 偶数 的整数数组 nums ，同时还有一个空数组 arr 。Alice 和 Bob 决定玩一个游戏，游戏中每一轮 Alice 和 Bob 都会各自执行一次操作。游戏规则如下：

• 每一轮，Alice 先从 nums 中移除一个 最小 元素，然后 Bob 执行同样的操作。

• 接着，Bob 会将移除的元素添加到数组 arr 中，然后 Alice 也执行同样的操作。

• 游戏持续进行，直到 nums 变为空。

返回结果数组 arr 。

示例 1：

输入：nums = [5,4,2,3]
输出：[3,2,5,4]
解释：第一轮，Alice 先移除 2 ，然后 Bob 移除 3 。然后 Bob 先将 3 添加到 arr 中，接着 Alice 再将 2 添加到 arr 中。于是 arr = [3,2] 。
第二轮开始时，nums = [5,4] 。Alice 先移除 4 ，然后 Bob 移除 5 。接着他们都将元素添加到 arr 中，arr 变为 [3,2,5,4] 。

示例 2：

输入：nums = [2,5]
输出：[5,2]
解释：第一轮，Alice 先移除 2 ，然后 Bob 移除 5 。然后 Bob 先将 5 添加到 arr 中，接着 Alice 再将 2 添加到 arr 中。于是 arr = [5,2] 。

答案

"""
你有一个下标从 0 开始、长度为 偶数 的整数数组 nums ，同时还有一个空数组 arr 。Alice 和 Bob 决定玩一个游戏，游戏中每一轮 Alice 和 Bob 都会各自执行一次操作。游戏规则如下：

每一轮，Alice 先从 nums 中移除一个 最小 元素，然后 Bob 执行同样的操作。
接着，Bob 会将移除的元素添加到数组 arr 中，然后 Alice 也执行同样的操作。
游戏持续进行，直到 nums 变为空。
返回结果数组 arr 。

示例 1：
输入：nums = [5,4,2,3]
输出：[3,2,5,4]
解释：第一轮，Alice 先移除 2 ，然后 Bob 移除 3 。然后 Bob 先将 3 添加到 arr 中，接着 Alice 再将 2 添加到 arr 中。于是 arr = [3,2] 。
第二轮开始时，nums = [5,4] 。Alice 先移除 4 ，然后 Bob 移除 5 。接着他们都将元素添加到 arr 中，arr 变为 [3,2,5,4] 。

示例 2：
输入：nums = [2,5]
输出：[5,2]
解释：第一轮，Alice 先移除 2 ，然后 Bob 移除 5 。然后 Bob 先将 5 添加到 arr 中，接着 Alice 再将 2 添加到 arr 中。于是 arr = [5,2] 。
"""


class Solution(object):
    def numberGame(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        #升序排列整数数组
        nums.sort()
        #初始化一个空数组
        arr = []
        #交换相邻整数
        for i in range(0, len(nums), 2):
            arr.append(nums[i + 1])
            arr.append(nums[i])
        return arr


if __name__ == '__main__':
    nums = [5, 4, 2, 3]
    print(Solution().numberGame(nums))

if __name__ == '__main__':
    nums = [2, 5]
    print(Solution().numberGame(nums))

结果分析

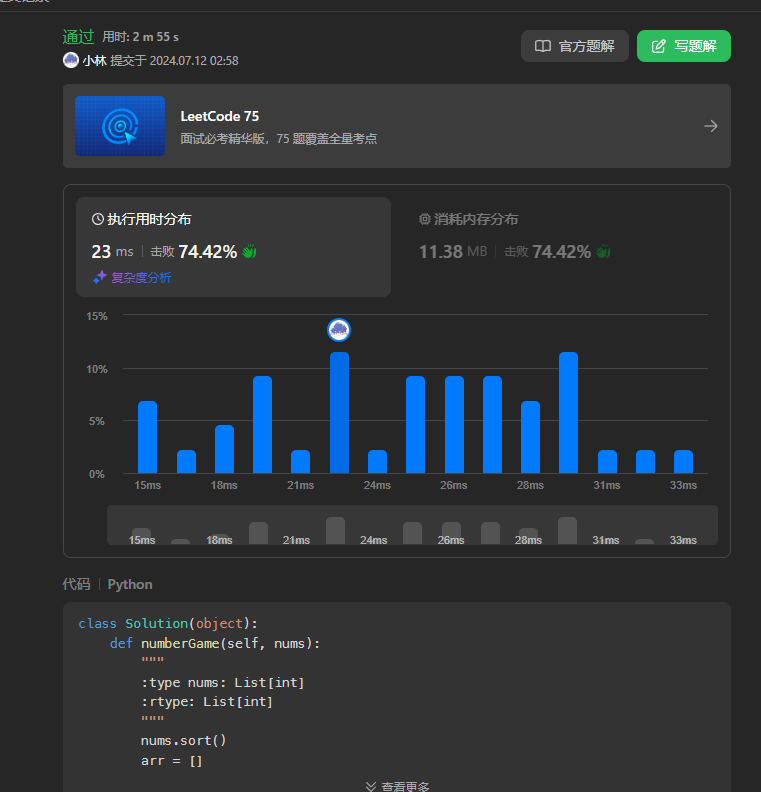
时间复杂度：

排序操作：nums.sort() 通常使用的是快速排序或归并排序等高效算法，平均时间复杂度为 O(nlogn)，其中 n 是 nums 的长度。

循环操作：执行了一个循环，循环次数为 len(nums) // 2，因为每次循环都会处理两个元素，所以实际上只需要遍历 nums 的一半长度。循环内的操作都是常数时间复杂度的，所以这部分的时间复杂度为 O(len(nums) // 2)，即 O(n)

整体来看，整个函数的时间复杂度主要由排序操作决定，因此最终的时间复杂度为 O(nlogn)。

空间复杂度：

排序操作：在排序过程中，Python 的内置排序算法可能会使用额外的内存空间，这部分空间复杂度通常是 O(n)。因为排序通常需要一个额外的数组来存储排序后的元素。

新列表 arr：创建了一个新列表 arr 来存储交换后的元素。这部分空间复杂度也是 O(n)，因为 arr 的长度与 nums 的长度相同。

整体来看，空间复杂度为 O(2n)，即 O(n)